土砂崩落やインフラ点検などで最適化するためにAI性能を評価するには？【土木×AI第13回】：“土木×AI”で起きる建設現場のパラダイムシフト（13）（2/2 ページ）

[阿部雅人（土木学会 AI・データサイエンス実践研究小委員会 副委員長），BUILT]

未検出や誤検出をなくすためには、適合率や再現率に注目

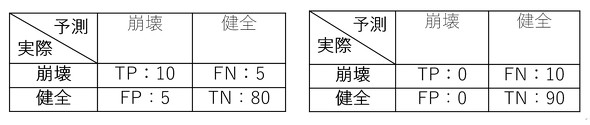
　それでは簡単な例で考えてみましょう。以下の4例では、正解率は全て90％で同じとなっています。例1では、崩壊と予測されたサンプルは現実でも崩壊しているので適合率は100％ですが、健全と予測されたものにも崩壊しているサンプルが含まれているため、再現率は50％になっています。

　また、例2には未検出はありませんが、崩壊と予測されたもののうち、半数は健全なので適合率は50％。例3は誤検出／未検出とも同数が含まれており、適合率／再現率とも66.7％となります。

　このように、同じ正解率でも適合率や再現率は、さまざまの値をとることがあります。未検出をなくしたければ再現率、誤検出をなくしたい場合には適合率に注目する必要があります。

例1　適合率：100％／再現率：50％／IoU：50％（左表）、例2　適合率：50％／再現率：100％／IoU：50％（右表）

例3　適合率：66.7％／再現率：66.7％／IoU：50％（左表）、例4　全て「健全」と予測／IoU：0％（右表）

　ここで、最初に示した航空写真をもとにした土砂災害検出結果を改めて見てみましょう。実際には、写真全体の面積に対し、土砂崩壊している面積はかなり小さいのが普通です。もともと実際に崩壊しているサンプルが健全のサンプルに比べて圧倒的に少ない「データの不均衡」が生じていると、例4のように、単に全て「健全」と推定するだけで高い正解率となってしまいます。

　データの不均衡は、災害では一般的ですし※4、インフラ点検にAIを適用する際も、構造物全体からみれば損傷が発生している部位はごく一部でしかありません※5。そのため、データの不均衡があるインフラや防災に関する問題では、適合率や再現率が一層重要となります。

※4 「防災応用の観点からの機械学習の研究動向」宮本崇,浅川匡,久保久彦,野村泰稔,宮森保紀／AI・データサイエンス論文集1巻J1号p242-251／「科学技術情報発信・流通総合システム（J-STAGE）」／2020年

※5 「コンクリートのひび割れおよび剥離・剥落の点検技術の評価に関する研究」松村隆爾,杉崎光一,鎌田敏郎,松田浩／土木学会論文集F4（建設マネジメント）72巻3号p73-83／「科学技術情報発信・流通総合システム（J-STAGE）」／2016年

　冒頭の例のようなセマンティックセグメンテーションやバウンディングボックスなどの物体検出AIの精度を評価するには、下図のようなIoU（Intersection over Union）という考え方も有効です。

　実際の領域と予測された領域の重なり合う部分の面積の割合を表したもので、完全に重なると100％となります。上の例1〜3では、FNやFPの分布が異なりますが、TPの占める割合は同じなのでIoUは全て50％という同じ値になっています。一方で、全て健全と予測している例4では0％となっています。

IoU（Intersection over Union）

　AIの評価には、他にも、特異度やF値などの指標も用いられます。いずれも、混同行列から導かれるもので、適合率（precision）と再現率（recall）の考え方が基本となります。対象や問題に適した定量的な評価を行うことで、AIの開発をより効果的で効率的に行うことができるようになるのです。

著者Profile

阿部 雅人／Masato Abe

ベイシスコンサルティング 研究開発室 チーフリサーチャー。防災科学技術研究所 客員研究員。土木学会 構造工学委員会 構造工学でのAI活用に関する研究小委員会 副委員長を務めた後、現在はAI・データサイエンス実践研究小委員会 副委員長。インフラメンテナンス国民会議 実行委員も兼任。

近著に、「構造物のモニタリング技術」（日本鋼構造協会編／コロナ社）がある。

★連載バックナンバー：

『“土木×AI”で起きる建設現場のパラダイムシフト』

　■第12回：【第12回】「見えないものを見る」AIとセンシング技術の可能性

　■第11回：【第11回】“スマートシティー”を実現するAI、車種別の交通量解析など最新研究

　■第10回：【第10回】自然災害を未然に防ぐAI最新研究、降雨量や斜面崩壊を“LSTM”で予測