メディア

河川氾濫などの災害を予測する「物理知識を取り入れたニューラルネットワーク」【土木×AI第26回】：“土木×AI”で起きる建設現場のパラダイムシフト（26）（1/2 ページ）

今回は、物理知識を取り入れたニューラルネットワーク「PINNs」を用い、河川氾濫や地滑りなどの自然災害を予測する研究を紹介します。

» 2024年07月19日 10時00分公開

[阿部雅人（土木学会 AI・データサイエンス実践研究小委員会副委員長），BUILT]

　土木工学では、構造物が荷重を受ける際の変形や、河川での水の流れなどのさまざまな自然現象を扱います。こうした自然現象は物理学的にモデル化可能で、微分方程式で表せます。構造解析や水理解析のソフトウェアでは、構造物や河川などの形状や条件に合わせて、微分方程式を数値計算で解いています。そのような問題にも、人間の脳を模した機械学習プログラム「ニューラルネットワーク」の適用が考えられています。

物理知識を取り入れたニューラルネットワーク「PINNs」とは何か？

　すぐに思い浮かぶのは、「微分方程式のインプットとアウトプット（解）の関係を再現するようにニューラルネットワークを学習させればよいのでは」というアイデアです。そのようなアプローチは、一般に「サロゲート（代理）」モデルと呼ばれています。ただし、単にインプットとアウトプットから学習するだけでは、方程式の情報が含まれていないため、結果が物理的に成立しない可能性があります。

　問題解決の方法として、「PINNs（Physics-Informed Neural Networks：物理知識を取り入れたニューラルネットワーク）」※1が提案され、関連した研究が進んでいます。

※1 “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations" - ScienceDirect

★連載バックナンバー：

『“土木×AI”で起きる建設現場のパラダイムシフト』

本連載では、土木学会構造工学でのAI活用に関する研究小委員会で副委員長を務める阿部雅人氏が、AIと土木の最新研究をもとに、今後の課題や将来像について考えていきます。

　PINNsは、微分方程式の条件とニューラルネットワークで得られる結果との誤差を損失関数として学習に取り入れ、物理法則を満たそうとするものです。PINNsによって、計算を高速化したり、計測データに基づいて材料特性を推定する「逆解析」をしたりすることが可能です※2,3。

※2 「Physics-Informed Neural Networksによる1次元連続体の動的解析」宮本崇,西尾真由子,全邦釘／AI・データサイエンス論文集2巻J2号p152-156／「科学技術情報発信・流通総合システム（J-STAGE）」／2021年

※3 「波動解析や逆問題および非破壊評価におけるAI・データサイエンス活用の動向」斎藤隆泰,廣瀬壮一／AI・データサイエンス論文集4巻3号p852-866／「科学技術情報発信・流通総合システム（J-STAGE）」／2023年

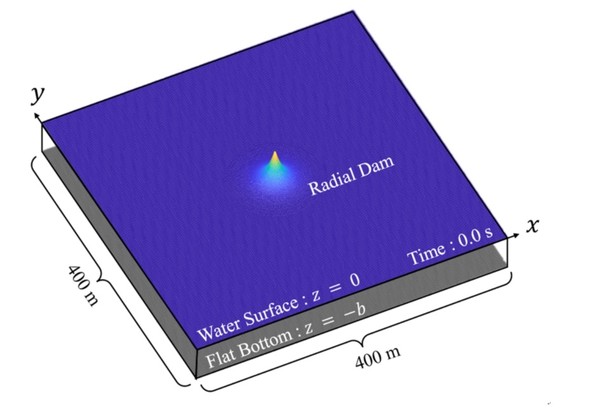
　文献4では、津波や洪水氾濫（はんらん）解析の基礎方程式となる浅水方程式について、従来の数値解析とPINNsを比較しています。下図のような、中央に山がある特殊な水位を初期条件として与え、その後の水位の動きを計算する問題を取り上げています。強制的に水位を与えた後、自由に動くようにする問題設定ゆえに、ダムが突然なくなった後の水位の変化になぞらえて「ダムブレーク」問題ともよばれます。

初期水位分布（二次元ダムブレーク問題）　出典：※4

※4 「Physics-Informed Neural Networksによる浅水波伝播シミュレーションに関する基礎研究」増田和輝,金澤剛／AI・データサイエンス論文集4巻3号p26-35／「科学技術情報発信・流通総合システム（J-STAGE）」／2023年

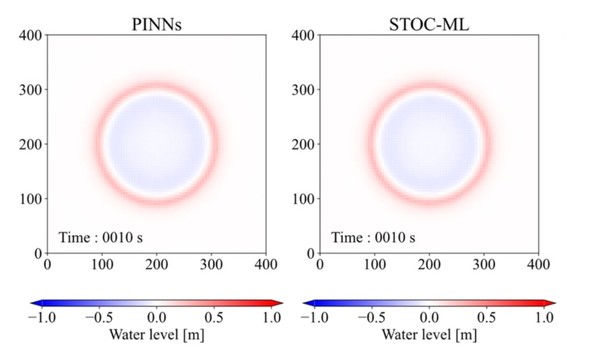
　下図は、PINNsと物理モデルによる高精度の数値計算で得た水位予測の結果比較です。数値計算結果を再現できており、PINNsが有効だと分かります。PINNsでは、物理モデルによる数値計算に比べ、事前学習は必要ですが、計算自体は短時間で可能となります。一方、学習した範囲外の条件への適用などが課題となります。